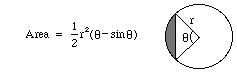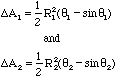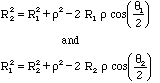INTRODUCTION
Eclipsing binary stars are just one several types of variable stars. These
stars appear as a single point of light to an observer, but based on its
brightness variation and spectroscopic observations we can say for certain that
the single point of light is actually two stars in close orbit around one
another. The variations in light intensity from eclipsing binary stars is
caused by one star passing in front of the other relative to an observer. If
we assume that the stars are spherical and that they have circular orbits, then
we can easily approximate how the light varies as a function of time for
eclipsing binary stars. These calculations can be performed in a relatively
short computer program.
THE ORBIT AND STAR PARAMETERS
A brightness versus time plot for a variable star is know as light
curve. For close binary systems, time is usually expressed as phase, for
which one unit of time is the orbital period. Measured light curves for
periodic variable stars are usually "folded", which means that successive
cycles are plotted atop one another. An example of an experimentally measured
light curve is given in Figure 1. Note that the vertical axis of the graph is
labeled "magnitude" which is a logarithmic scale of brightness.
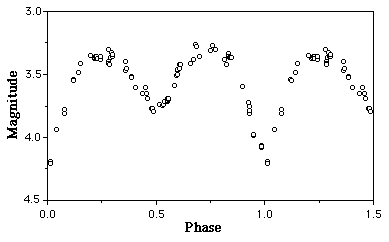
Figure 1: Photometry of Beta Lyrae in 1992-1993.
The shape of the light curve for an eclipsing binary star system depends
mostly on the relative brightness and size of the two stars as well as their
orbital inclination as seen from Earth. We will now see how you can use simple
geometry to generate a light curve. For this simple spherical star model, the
parameters that are needed to generate a light curve are:
i = Orbital Inclination
M1,
M2 = Masses of the Stars
L1,
L2 = Luminosities of the Stars
R1,
R2 = Radii of the Stars
The orbital inclination is measured relative to the observer in degrees and is
90 degrees for edge-on orbits. The star masses and luminosities can be
expressed in arbitrary units and the star radii will be expressed in terms of a
fraction of the orbit radius of the binary star orbit.
THE ECLIPSE EQUATIONS
If the orbits of the binary stars are assumed to be circular orbits then the
coordinates of star 1
(x1,y1,z1) and
star 2 (x2,y2,z2) can be found using the
following equations:
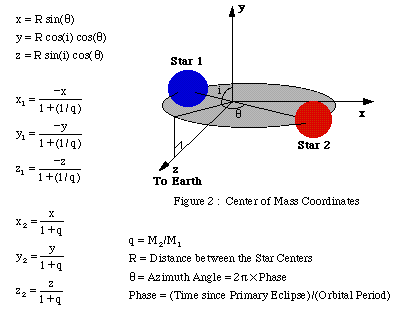
The x and y positions of the two stars can be used in a computer program
to draw the stars on the screen and the z coordinate can be used to determine
which star is in front
during an eclipse. The equations above are discussed in books like Herbert
Goldstein's Classical Mechanics [1] or Jerry B.
Marion's Classical Dynamics [2].
Luminosity is defined to be the amount of energy escaping from a star's
surface per unit time. The energy flux, F, at the surface a star is the amount
of energy radiated per unit area per unit time. For spherical, uniformly lit
stars we can write
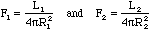
If we ignore limb darkening, then we can approximate the measured brightness of
the binary star system as seen by an observer as
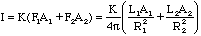
where A1 and
A2 are the
areas of the star disks seen by the observer and K is a
constant that can be determined from the area of the observer's detector and
the distance between the Earth and the binary star system.
A1 and
A2 can be
found by considering the geometry of the eclipses. To find these areas we will
need to know the apparent distance between the two stars as seen by an
observer. Using Figure 2, we see that this distance is
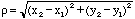
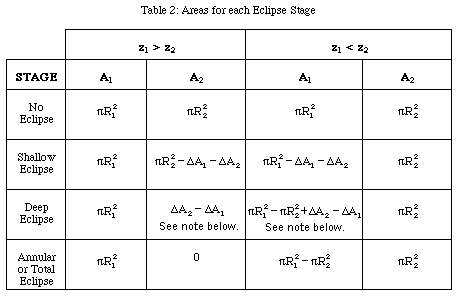
The values for A1 and
A2 for the different
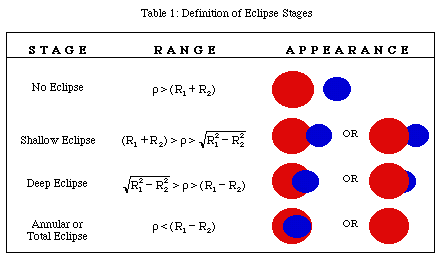
stages of the eclipses are given in the tables below.
These tables are only valid when R1 >
R2.
The area of a portion of a circle cut by a line segment can be found using the following
equation:
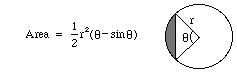 where r is the radius of the circle and theta (in radians) is the angle
subtended by the line segment.
Therefore,
where r is the radius of the circle and theta (in radians) is the angle
subtended by the line segment.
Therefore,
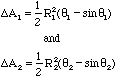
The theta's can be found using the law of cosines as follows:
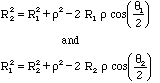
Note: The theta's here are assumed to be between 0 and 180 degrees.
If your computer computes theta's that are greater than 180 degrees, then
you will need to subtract them from 360 degrees to get the correct values.
Another Simpler Approach: If your computer computes theta's that are greater than 180 degrees, then
you may also replace (not swap) the equations for the Deep Eclipse with those
from the Shallow Eclipse in Table 2 above.
SUMMARY AND RESULTS
Given i,
M1,
M2,
L1,
L2,
R1,
R2,
and the phase of the orbit
one can use the equations above to determine the relative positions
of the stars, (x1,y1,z1) and
(x2,y2,z2), and the brightness of the system, I.
Figure 3 shows an example light curve generated using
the equations above.
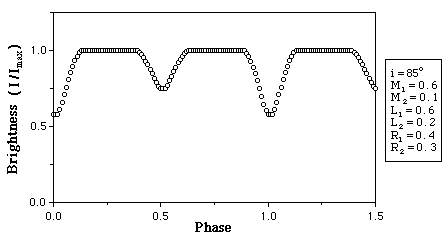
Figure 3: An example light curve with
masses and luminosities expressed in arbitrary units and the star radii
expressed in terms of a fraction of the orbit radius of the binary star orbit
You will notice that the masses have no effect on the light
curve for this simple model. However, one will see the effects of the masses
by observing the stars in orbit about the center of mass in an animation.
For a large
mass ratios q=M2/M1
(M2 >> M1), star 2 will not move much. For small mass
ratios, star 1 will not move much.
The orbital inclination, i, will effect the depth of the eclipses with the
minimum possible intensities occurring when the orbital inclination is 90
degrees. The radii and luminosities of the stars also effect the depth of the
eclipses as well as the general shape of the light curves.
There is software and code available that use
the simple model discussed here. To improve this model, the effects
of limb darkening, tidal distortion, elliptical orbits and other phenomena
can be considered. There are several books and articles that discuss
these effects
[3,4,5,6,7].
- Herbert Goldstein, Classical Mechanics, Second Edition, Addison-Wesley, 1981,
Equations 3-64, 3-8 and 3-2.
- Jerry B. Marion, Classical Dynamics, Equations 7.52, 7.10, and 7.3.
- David Gossman, "Light Curves and Their Secrets", Sky & Telescope, October 1989, p.410.
- Robert E. Wilson and Edward J. Devinney, "Realization of Accurate
Close-Binary Light Curves: Application to MR Cygni",
Astrophysical Journal, vol. 166, 1971, p. 605-619.
- Robert E. Wilson, "Eccentric Orbit Generalization and Simultaneous
Solution of binary Star Light and Velocity Curves",
Astrophysical Journal, vol. 234, 1979, p. 1054-1066.
- Zdenek Kopal, Language of the Stars, D. Reidel, 1979.
- Zdenek Kopal, The Roche Problem, Kluwer Academic, 1989.
Notes: The equations in this document were created using MathType 3.0.
A Microsoft Word document was created with the equations and figures.
The document was then saved as an RTF (rich text format) file from Microsoft
Word and then
RTFtoHTML
was used to create the HTML file.
This document also uses the HTML subscript feature <sub> </sub>.
Back to Eclipsing
Binary Stars
Dan Bruton
astro@sfasu.edu